所谓的DFS就是深度优先遍历,一条路走到黑,走到无路可走了才会选择回头,
DFS俗称爆搜,深搜,最重要的就是我们按照什么顺序来把题目全部遍历一下。DFS对应的流程是一个树的结构,DFS的精髓在于递归求解的思路以及回溯的处理。针对搜索的过程,又有重要的剪枝优化。必要的剪枝优化对DFS的顺序执行有很大的作用。
DFS的过程就是沿着树的深度遍历树的节点,尽可能深的搜索树的分支,当节点v的所在边都搜过,搜索回溯到发现节点v的那条边的起始节点。
DFS使用的数据结构是栈,时间复杂度是O(n),DFS不具有最短性,也就是DFS搜到的路径不一定是最短路。
DFS的模板框架
function dfs(当前状态){
if(当前状态 == 目的状态){
···
}
for(···寻找新状态){
if(状态合法){
vis[访问该点];
dfs(新状态);
?是否需要恢复现场->vis[恢复访问]
}
}
if(找不到新状态){
···
}
}
剪枝优化
剪枝是在不跳过最优解的情况下,采取必要的手段跳过不含有最优解的分支,减少搜索的次数,减少程序运行的时间。
剪枝优化这里就不赘述了。
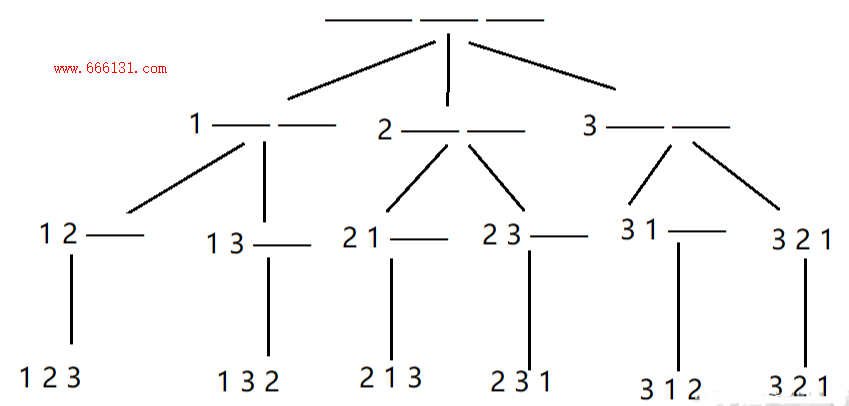
DFS经典案例-全排列问题
给定一个整数 nn,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤7
输入样例:
3
输出样例:
1 2 31 3 22 1 32 3 13 1 23 2 1
思路
利用DFS一层一层搜,搜完了就回溯,然后再根据结束条件判断是否搜索完毕
DFS详解
代码实现
#include <iostream>
using namespace std;
const int N=10;
int p[N];
int n;
bool st[N];
void dfs(int u)
{
//结束条件
if(u>n)
{
for(int i=1;i<=n;i++)
cout<<p[i]<<” “;
cout<<endl;
return;
}
//寻找新节点
for(int i=1;i<=n;i++)
{
//判断是否合法
if(!st[i])
{
p[u]=i;
st[i]=true;
dfs(u+1);
st[i]=false;
}
}
}
int main()
{
cin>>n;
dfs(1);
return 0;
}
深度优先搜索(DFS)
这块内容很重要哦,为了方便大家理解,先举一个(来自胡凡、曾磊老师编写的《算法笔记》一书)的栗子。
举个栗子:
设想我们现在以第一视角身处一个巨大的迷宫当中,没有上帝视角,没有通信设施,更没有热血动漫里的奇迹,有的只是四周长得一样的墙壁。于是我们只能自己想办法走出去。如果迷失了内心,随便乱走,那么很可能会被四周完全相同的景色绕晕在其中,这时只能放弃所谓的侥幸,而去采取下面这种看上去很盲目但实际上会很有效的方法。
以当前所在位置为起点,沿着一条路向前走,当碰到岔道口时,选择其中一条岔道前进。如果岔路中存在新的岔道口,那么仍然按照上面的方法枚举新岔道口的每一条岔路。这样,只要迷宫存在出口,那么这个方法一定能找到它。
可能有铁汁会问,如果在第一个岔道口选择了没有出路的分支,而这个分支比较深,并且路上多次出现了新的岔道口,那么当发现这个分支是个死分支之后,如何退回到最初的这个岔道口?其实方法很简单,只要让自己的右手,始终贴着右边的墙壁一路往前走,那么自动会执行上面这个走法,并且最终一定能找到出口。
你看下图:
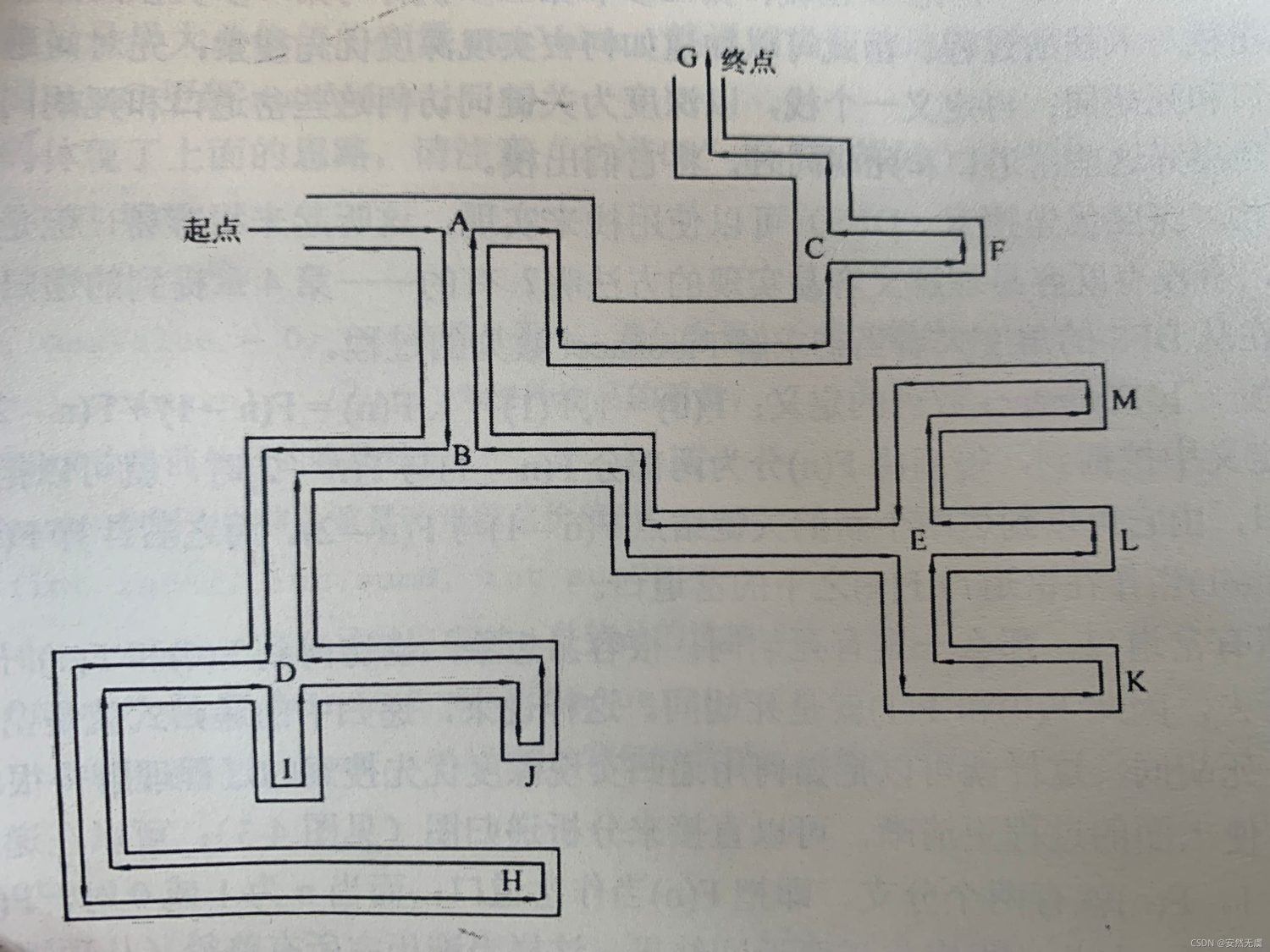
由图可知,从起点开始前进,当碰到岔道口时,总是选择其中一条岔路前进(注意哦,这里总是选择最右手边的岔路),在岔路上如果又遇到新的岔道口,仍然选择新岔道口的其中一条岔路前进,直到碰到死胡同才回退到最近的岔道口选择另一条岔路。也就是说,当碰到岔道口时,总是以“深度”作为前进的关键词,不碰到死胡同就不回头,因此把这种搜索的方式称为深度优先搜索。
从这个迷宫的例子还可以注意到,深度优先搜索会走遍所有路径,并且每次走到死胡同就代表一条完整路径的形成。这就是说,深度优先搜索是一种枚举所有完整路径以遍历所有情况的搜索方法。
总结何为深度优先搜索:
从根节点开始,尽可能深的搜索每一个分支,把一个分支的结果搜索完,再去看另一个分支。形象来说:“一条路走到底,不撞南墙不回头”。
【敲黑板】:上面的内容可能有点绕,所以建议铁汁们最好认真看个三遍这样子,好好去理解,毕竟这一章属于拔高部分,可能稍微难理解些,但做题目后会发现其实不难,不信的话,往后看。不对不对,先把上面弄得差不多了再朝后看…
问:用什么方法能更好的实现深度优先搜索呢?
其实要想既容易理解又容易实现深度优先搜索非递归莫属